Problem Set 3. DAGs.
Relevant material will be covered by Sep 21. Problem set is due Sep 28.
To complete the problem set, copy this code into a .Rmd and complete the homework. Omit your name so we can have anonymous peer feedback. Compile to a PDF and submit the PDF on Canvas.
Note: For this problem set only, you alternatively may complete the homework by hand. This is because you are welcome to draw DAGs by hand instead of producing them by code. If you do this, scan or take a picture of your document.
1. True or False
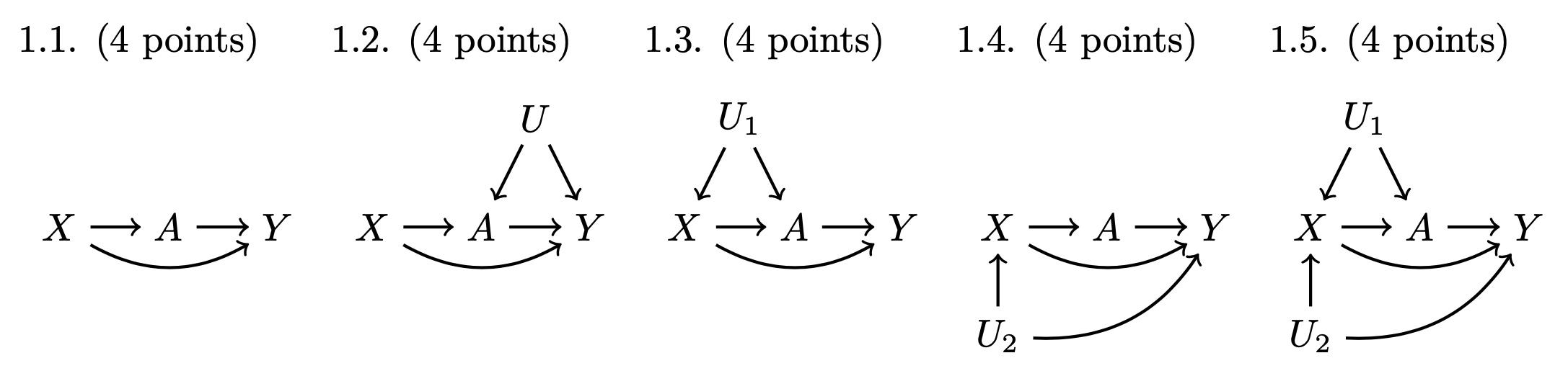
For 1.1–1.5, answer True or False: \(X\) is a sufficient adjustment set to identify the causal effect of \(A\) on \(Y\). Explain in one sentence. If False, state the backdoor path that is unblocked conditional on \(X\). A path is a linear series of nodes connected by arrows; see examples in 1.6 and 1.7.
2. Draw a DAG (10 points)
A researcher comes to you with a proposal: identify the causal effect of \(A\) on \(Y\) by adjusting for any variable \(X\) that predicts \(A\) and also predicts \(Y\). They propose that machine learning can thus solve causal identification for us.
The researcher is wrong. Show them why. Draw a DAG in which
- the effect of \(A\) on \(Y\) is unconfounded
- a variable \(X\) is statistically associated with \(A\)
- a variable \(X\) is statistically associated with \(Y\)
- but one does not need to adjust for \(X\) to identify the causal effect
3. Using DAGs in a new context
DAGs are not just useful for causal inference: they can be useful whenever we need to know whether one variable is statistically independent of another. This is true, for example, when drawing inference about a population from a sample.
A researcher uses an opt-in online web survey to draw inference about support for President Biden. They ask respondents: ``Do you approve of President Biden’s performance in office?’’ with the answer choices Yes/No. The researcher also gathers data on two demographic characteristics: whether the respondent completed college and current employment. They write:
My sample is not representative. Suppose for every person in the population, \(S\) denotes whether they are included in my sample. Then \(S\) is related to their approval of President Biden (\(Y\)).
However, I believe my sample is representative when I look at a set of people who all take the same value along college completion and employment, such as those who finished college and are currently employed. If these variables are \(X_1,X_2\), I believe this independence statement: \(S\) is independent of \(Y\) given \(X_1,X_2\). I will therefore get population estimates by a procedure with several steps: use my sample to estimate the mean outcome \(E(Y\mid \vec{X} = \vec{x})\) in each stratum, then use Census data to estimate the size of each stratum \(P(\vec{X} = \vec{x})\) in the population, then estimate \(E(Y) = \sum_{\vec{x}}E(Y\mid \vec{X} = \vec{x})P(\vec{X} = \vec{x})\).
This researcher’s reasoning is a common strategy known as post-stratification. This question is about formalizing a set of conditions under which the researcher is right and wrong.
Before you begin, we want to emphasize one aspect of the researcher’s assumption that is different from the exchangeability assumption for causal inference.
- for causal claims, we assume conditional exchangeability: \(A\) independent of \(Y^a\) given \(\vec{X}\)
- involves the potential outcome \(Y^a\)
- holds if the only unblocked paths between \(A\) and \(Y\) are causal paths
- for sample-to-population inference, we assume conditionally independent sampling \(S\) independent of \(Y\) given \(\vec{X}\)
- involves the factual outcome \(Y\); there is no intervention here
- holds if there are no unblocked paths between \(S\) and \(Y\)
Although the assumption is different, the principles of DAGs are still relevant.